Ajatusketjukehottaminen
Ajatusketjukehottaminen
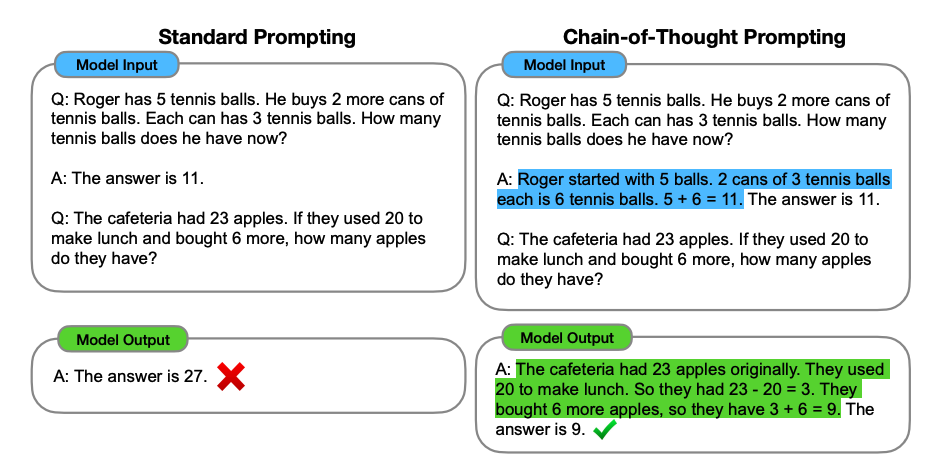
Kuvan lähde: Wei ym. (2022) (opens in a new tab)
Wei ym. (2022) (opens in a new tab) julkaisussa esitelty ajatusketjua hyödyntävä kehotesuunnittelu (CoT) mahdollistaa monimutkaisemman päättelyn välillisten päättelyvaiheiden avulla. Sen avulla voidaan yhdistää vähäisen ohjauksen kehottaminen parempien tulosten saamiseksi monimutkaisemmissa tehtävissä, jotka vaativat päättelyä ennen vastaamista.
Kehote:
Parittomat luvut tässä ryhmässä summattuna antavat parillisen luvun: 4, 8, 9, 15, 12, 2, 1.
A: Kaikkien parittomien lukujen (9, 15, 1) summa on 25. Vastaus on Epätosi.
Parittomat luvut tässä ryhmässä summattuna antavat parillisen luvun: 17, 10, 19, 4, 8, 12, 24.
A: Kaikkien parittomien lukujen (17, 19) summa on 36. Vastaus on Tosi.
Parittomat luvut tässä ryhmässä summattuna antavat parillisen luvun: 16, 11, 14, 4, 8, 13, 24.
A: Kaikkien parittomien lukujen (11, 13) summa on 24. Vastaus on Tosi.
Parittomat luvut tässä ryhmässä summattuna antavat parillisen luvun: 17, 9, 10, 12, 13, 4, 2.
A: Kaikkien parittomien lukujen (17, 9, 13) summa on 39. Vastaus on Epätosi.
Parittomat luvut tässä ryhmässä summattuna antavat parillisen luvun: 15, 32, 5, 13, 82, 7, 1.
A:Tulos:
Kaikkien parittomien lukujen (15, 5, 13, 7, 1) summa on 41. Vastaus on Epätosi.Kun tarjoamme päättelyvaiheen, saamme täydellisen tuloksen. Itse asiassa tehtävän ratkaisemiseen riittää vielä vähemmän esimerkkejä. Yksi esimerkki näyttää olevan riittävä:
Kehote:
Parittomat luvut tässä ryhmässä summattuna antavat parillisen luvun: 4, 8, 9, 15, 12, 2, 1.
A: Kaikkien parittomien lukujen (9, 15, 1) summa on 25. Vastaus on Epätosi.
Parittomat luvut tässä ryhmässä summattuna antavat parillisen luvun: 15, 32, 5, 13, 82, 7, 1.
A:Tulos:
Kaikkien parittomien lukujen (15, 5, 13, 7, 1) summa on 41. Vastaus on Epätosi.Tutkijoiden mukaan tämän on emergentti kyky, joka ilmenee riittävän suurilla kielimalleilla.
Nollakehote CoT

Kuvan lähde: Kojima ym. (2022) (opens in a new tab)
Yksi tuore idea on nollaoppimis CoT zero-shot CoT (opens in a new tab) (Kojima ym. 2022) joka periaatteessa sisältää tekstin "Mietitään askel askeleelta" lisäämisen alkuperäiseen kehotteeseen. Kokeillaan yksinkertaista ongelmaa ja katsotaan, miten malli suoriutuu:
Kehote:
Menin kauppaan ja ostin 10 omenaa. Annoin 2 omenaa naapurille ja 2 huoltomiehelle. Sen jälkeen menin ja ostin 5 omenaa lisää ja söin yhden. Kuinka monta omenaa minulle jäi?Tulos:
Sinulla on jäljellä 11 omenaa.
Aluksi sinulla oli 10 omenaa, mutta annoit 2 naapurillesi ja 2 huoltomiehelle, jolloin sinulla oli jäljellä 6 omenaa. Sen jälkeen ostit lisää 5 omenaa, jolloin sinulla oli yhteensä 11 omenaa. Söit yhden omenan, joten jäljellä oli vielä 10 omenaa.Vastaus on väärä, ainakin aluksi! Tämä toimii hyvänä esimerkkinä tavasta jolla suuret kielimallit toimivat. Kun malli käytännössä vain ennustaa seuraavaa oikeaa merkkiä, tuloksen alussa ja lopussa on potentiaalisesti eroa. Kokeillaan nyt erikoisella kehotteella.
Kehote:
Menin kauppaan ja ostin 10 omenaa. Annoin 2 omenaa naapurille ja 2 korjaajalle. Sen jälkeen menin ja ostin 5 lisää omenaa ja söin 1. Kuinka monta omenaa minulle jäi?
Mietitään askel askeleelta.Tulos:
Selvä, mennään askel askeleelta:
Aluksi ostit 10 omenaa.
Sitten annoit 2 omenaa naapurille, joten sinulle jäi 10 - 2 = 8 omenaa.
Annoit 2 omenaa huoltomiehelle, jolloin sinulle jäi 8 - 2 = 6 omenaa.
Sen jälkeen ostit 5 lisää omenaa, joten sinulla oli yhteensä 6 + 5 = 11 omenaa.
Lopuksi söit 1 omenan, jolloin sinulle jäi 11 - 1 = 10 omenaa.
Sinulle jäi siis yhteensä 10 omenaa.Yksinkertainen kehote osoittautuu tehokkaaksi tässä tehtävässä. Tämä on erityisen hyödyllistä, jos sinulla ei ole montaa esimerkkiä joita voit käyttää kehotteessa.